模板匹配、特征点匹配、相位法

一、模板匹配

二、 特征点匹配

特征点检测：SIFT、ORB、SURF

  • SIFT（尺度不变）：精度高，计算量大。
  • ORB（二进制）：速度快，适合实时应用。
  • SURF（加速版SIFT）：平衡速度与精度。

匹配方法：暴力匹配、FLANN

  • 暴力匹配（Brute-Force）：逐对比较，精度高但速度慢。
  • FLANN（近似最近邻）：适合大规模数据，需根据描述子类型调整参数（如KD树用于浮点，LSH用于二进制）。

SIFT描述子是基于梯度的方向直方图，而ORB用的是二进制描述子，比如BRIEF。二进制描述子的优势是计算速度快，因为比较的是二进制位的差异，可以用汉明距离来衡量相似性。而像SIFT这样的浮点型描述子，则用欧氏距离。这可能影响匹配的速度和准确性。

三、相位法

两幅图像在空域的平移对应频域的相位差，通过计算两幅傅里叶图像的互功率谱（Cross Power Spectrum），相位差会表现为一个脉冲峰值，其位置即为位移量。

输入2张刚性平移的图像：phase_img

输出偏移坐标：(-0.27,4.89)

WIKI解释：https://en.wikipedia.org/wiki/Phase_correlation

CV源码分析phasecorr.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
cv::Point2d cv::phaseCorrelate(InputArray _src1, InputArray _src2, InputArray _window, double* response)
{
    CV_INSTRUMENT_REGION();

    Mat src1 = _src1.getMat();
    Mat src2 = _src2.getMat();
    Mat window = _window.getMat();

    CV_Assert( src1.type() == src2.type());
    CV_Assert( src1.type() == CV_32FC1 || src1.type() == CV_64FC1 );
    CV_Assert( src1.size == src2.size);

    if(!window.empty())
    {
        CV_Assert( src1.type() == window.type());
        CV_Assert( src1.size == window.size);
    }

    int M = getOptimalDFTSize(src1.rows);
    int N = getOptimalDFTSize(src1.cols);

    Mat padded1, padded2, paddedWin;

    if(M != src1.rows || N != src1.cols)
    {
        copyMakeBorder(src1, padded1, 0, M - src1.rows, 0, N - src1.cols, BORDER_CONSTANT, Scalar::all(0));
        copyMakeBorder(src2, padded2, 0, M - src2.rows, 0, N - src2.cols, BORDER_CONSTANT, Scalar::all(0));

        if(!window.empty())
        {
            copyMakeBorder(window, paddedWin, 0, M - window.rows, 0, N - window.cols, BORDER_CONSTANT, Scalar::all(0));
        }
    }
    else
    {
        padded1 = src1;
        padded2 = src2;
        paddedWin = window;
    }

    Mat FFT1, FFT2, P, Pm, C;

    // perform window multiplication if available
    if(!paddedWin.empty())
    {
        // apply window to both images before proceeding...
        multiply(paddedWin, padded1, padded1);
        multiply(paddedWin, padded2, padded2);
    }

    // execute phase correlation equation
    // Reference: http://en.wikipedia.org/wiki/Phase_correlation
    dft(padded1, FFT1, DFT_REAL_OUTPUT);
    dft(padded2, FFT2, DFT_REAL_OUTPUT);

    mulSpectrums(FFT1, FFT2, P, 0, true);

    magSpectrums(P, Pm);
    divSpectrums(P, Pm, C, 0, false); // FF* / |FF*| (phase correlation equation completed here...)

    idft(C, C); // gives us the nice peak shift location...

    fftShift(C); // shift the energy to the center of the frame.

    // locate the highest peak
    Point peakLoc;
    minMaxLoc(C, NULL, NULL, NULL, &peakLoc);

    // get the phase shift with sub-pixel accuracy, 5x5 window seems about right here...
    Point2d t;
    t = weightedCentroid(C, peakLoc, Size(5, 5), response);

    // max response is M*N (not exactly, might be slightly larger due to rounding errors)
    if(response)
        *response /= M*N;

    // adjust shift relative to image center...
    Point2d center((double)padded1.cols / 2.0, (double)padded1.rows / 2.0);

    return (center - t);
}

注意上述源码中的fftShift(C); // shift the energy to the center of the frame.，同时也在halcon demo(phase_correlation_fft)中发现对反傅里叶变换之后的图像进行平移cyclic_shift_image，略有困惑对其展开分析

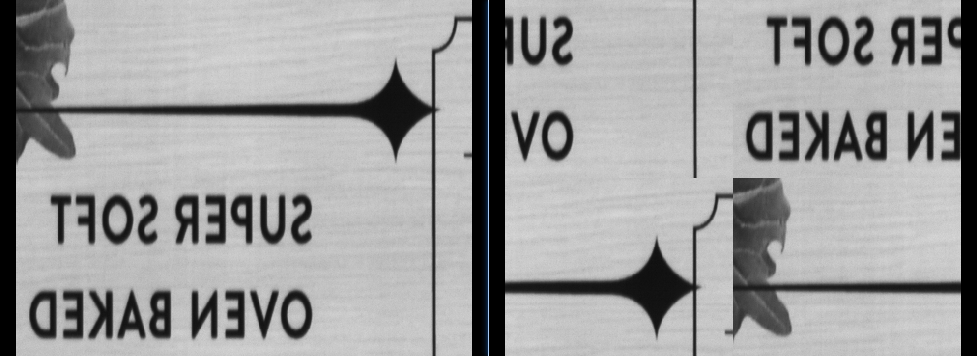
平移前后对比度（对角线上的像素区域互换了）

cpmpare_phase

halcon解释cyclic shift image做的原因： Since the phase correlation is cyclic, negative translations result in peaks in lower or right part of the image. If the translation is close 0 in one or two directions, the interpolation in local_max_sub_pix would therefore access wrong values because of its border treatment (which is not cyclic). To obtain a translation that is correct in all cases, we shift the phase correlation cyclically so that a zero translation corresponds to the center of the image. We then correct the coordinates returned by local_max_sub_pix.

1. 相位相关的循环性

相位相关法通过傅里叶变换计算图像的平移量。由于傅里叶变换的周期性，相位相关结果（峰值位置）是循环的。例如：

  • 负平移（如向左或向上移动）会表现为峰值出现在图像的右侧或底部（即循环移位后的等效位置）。
  • 零平移对应的峰值本应在原点（如左上角），但直接处理可能导致边界问题。

2. local_max_sub_pix的边界问题

local_max_sub_pix用于亚像素级峰值定位，但其默认的边界处理方式（如补零或镜像）不是循环的。当峰值靠近图像边缘时（如平移接近0），插值会访问无效的边界外像素，导致错误。

3. Halcon的解决方案：循环移位相位相关图

  • 步骤1：将相位相关结果循环移位 将零平移对应的峰值从原点（如左上角）移到图像中心。例如，通过fftshift操作，使得零平移的峰值位于(width/2, height/2)。
  • 步骤2：在移位后的图中定位峰值 此时，无论实际平移是正负，峰值都会远离边缘。例如，平移(-10, -5)的峰值会出现在中心附近的(width/2-10, height/2-5)，而非靠近边界的(width-10, height-5)。
  • 步骤3：修正坐标 将local_max_sub_pix返回的中心坐标系下的峰值坐标，转换为原始坐标系下的实际平移量。例如，若中心为(Cx, Cy)，找到的峰值为(Px, Py)，实际平移为(Px - Cx, Py - Cy)。

4. 关键操作示例

假设图像尺寸为512x512：

  • 原始相位相关图：零平移峰值在(0,0)。
  • 循环移位后：零平移峰值移至中心(256,256)。
  • 平移(-10, -5)的峰值：移位后位于(256-10, 256-5) = (246,251)。
  • 修正坐标：平移量为(246-256, 251-256) = (-10, -5)。

5. 总结

  • 循环移位：避免峰值靠近边界，确保插值有效。
  • 坐标修正：将中心坐标系转换回实际平移量。

通过这种方式，Halcon确保了在所有情况下（包括零平移附近）都能正确计算平移量。

时效性：50*50：3ms i7-9700k